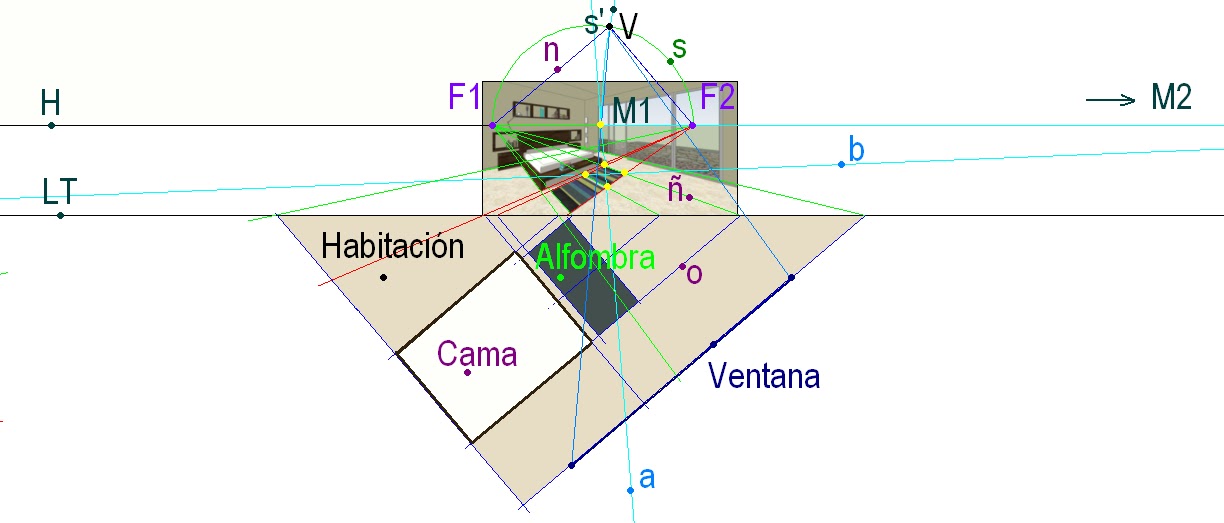
Partiendo de la foto o de un dibujo de una habitación, se trata de construir la verdadera forma de la misma, sus dimensiones y la distancia del punto de vista al plano del cuadro.
Se toma un cuadrado del dibujo, por ejemplo el que corresponde a un trozo de la alfombra, y se prolongan los lados de la misma (en el dibujo rayos de color rojo y verde), de esta forma obtenemos los dos puntos de fuga F1 F2 por donde pasa la línea del horizonte H. Hacemos las diagonales a b de este cuadrilátero (en el dibujo en color azul claro) y obtenemos en la intersección con el horizonte los dos puntos M1 M2. Hacemos dos semicircunferencias s s’, una que incide por el diámetro F1 F2 y la otra que incide por el diámetro M1 M2. La intersección de estas dos semicircunferencias determinan el punto de vista V y la perpendicular de este punto al horizonte define la distancia del punto de vista al plano del cuadro. Tomamos por un punto cualquiera del dibujo, por ejemplo el de un vértice inferior del mismo, una línea paralela al horizonte y la tomamos como línea de tierra LT. Para obtener la orientación de cada recta (por ejemplo la recta o), hacemos una paralela a la recta V-F1 por donde ñ corta a la línea de tierra, de esta forma tenemos que la dirección de una recta en el espacio viene definida por la dirección de la recta que pasa por el punto de vista V y el punto de fuga F1, en el dibujo tenemos estas dos líneas (n y V-F1 )abatidas y como ambas han sido giradas 90°, las dos permanecen paralelas. Con el otro punto de fuga F2 se procede de igual forma, para obtener la orientación de una recta se hace por la traza de la misma una recta paralela a la dirección que definen el punto de vista y el punto de fuga.
Para obtener la verdadera dimensión de cada línea del dibujo basta con hacer por el punto de vista V dos segmentos que pasen por el extremo de la línea en perspectiva del dibujo (por ejemplo los extremos de la ventana) de la que se quiere obtener la verdadera dimensión. La intersección de estas dos líneas con su correspondiente recta abatida de la figura en planta define la longitud exacta de la misma (en el dibujo segmento de color azul con el nombre ventana).
Restitución del cubo prescindiendo de las diagonales de la base. |
Para calcular el punto de vista dado un cubo y prescindiendo de hacer las diagonales de la base del cubo, podemos hacer la diagonal de una cara, por ejemplo la que definen los puntos SRDC. Esta diagonal que pasa por los puntos DR corta a la vertical que pasa por el punto de fuga F en el punto U. Haciendo centro en el punto de fuga F y tomando como radio la distancia FU hacemos una circunferencia hasta que corta a la semicircunferencia azul de diámetro FE, la que definen los dos puntos de fuga F E del cubo, obteniendo de esta forma en la intersección de ambos arcos el punto de vista V correspondiente a la perspectiva del cubo.
Un cuestión curiosa de este procedimiento es la siguiente, la perspectiva del cuadrado verde definida por los puntos SRDC tiene a U como punto métrico, ya que es la diagonal que pasa por los puntos RD. De esto parecería desprenderse que la distancia FU es realmente la distancia del punto de vista el plano del cuadro, y la proyección del punto de vista estaría en este caso sobre el punto de fuga F, sería una recta perpendicular al plano del cuadro desde este punto F con la distancia FU. En aparente contradicción tenemos que el punto de vista real cuando es un cubo pasa a ser el punto V, teniendo en consecuencia que la distancia del plano del cuadro al punto de vista es la distancia desde V hasta el plano del cuadro, que lógicamente es menor que la distancia UF. ¿Cómo es posible que en principio la misma figura tenga 2 puntos de vista distintos? La respuesta es muy sencilla, efectivamente la perspectiva del cuadrado tendría como punto de vista y punto principal la distancia UF, pero entendiendo que el plano del cuadrado fuera perpendicular al plano del cuadro, cosa que no sucede en el cubo, ya que en este caso las dos caras verde y roja son oblicuas respecto al plano del cuadro, mientras que en el cuadrado verde tendríamos que sería perpendicular al plano del cuadro siempre y cuando U fuera el punto de vista abatido y F el punto principal, cosa que realmente no sucede.
En síntesis, la perspectiva del cuadrado verde si tuviera por punto principal a F y por distancia del punto de vista el plano del cuadro UF, sería un cuadrado perpendicular al plano del cuadro, cosa que de ninguna manera puede suceder aquí, ya que la cara roja del cubo no aparece paralela al plano del cuadro, por lo que tenemos una perspectiva cónica oblicua y por tanto VF VE también son oblicuos respecto a la línea del horizonte o al plano del cuadro.
Restitución del cuboRestitución de un prisma en una perspectiva de cuadro inclinado.
Restitución de un prisma en una perspectiva de cuadro inclinado.
Para calcular las verdaderas dimensiones del prisma que como dato se aporta que sus caras son ortogonales entre sí, ya sabemos por la proyección gnomónica que hay una afinidad entre lo que sucede detrás del plano del cuadro y lo que acontece delante, por el punto de vista. El primer dato inmediato es que las paralelas se cortan en el infinito esto quiere decir que la perspectiva de esas líneas paralelas son otras líneas paralelas con un punto de fuga común, de esta forma dos aristas de una cara se cortan en un punto de fuga, otras dos aristas paralelas de la misma cara se cortan en otro punto de fuga y por ambos puntos de fuga pasa la recta límite o de horizonte del plano. Como esto sucede igualmente en las tres caras tenemos que de esta manera obtenemos los tres planos límites de las caras del prisma, para ello en el espacio se considera un prisma que pasa por el punto de vista y que corta al plano del cuadro segundo tres rectas que son las rectas limites de los tres planos correspondientes a la cara del prisma.
Para obtener la proyección del punto de vista P sobre el plano del cuadro basta con hacer por los tres puntos de fuga OEC rectas ortogonales a las rectas límites obteniendo en la intersección el ortocentro o punto principal P, que es la proyección del punto de vista sobre el plano del cuadro. El punto principal es la proyección del vértice de la pirámide por ser el ortocentro, ya que las tres caras del cubo que pasan por el punto de vista cumplen la condición de que cada una de las tres direcciones de las aristas del prisma forman entre sí 90°, y para que esto sea cierto en geometría tenemos que en el triángulo rojo correspondiente a las tres rectas límites, las alturas determinan el ortocentro, único punto que cumple esta condición.
Para determinar la posición exacta del punto de vista, se puede abatir el plano que contiene al punto principal y cuya traza es la recta LE. Al construir una semicircunferencia cuyo diámetro es este segmento tenemos que la perpendicular por el punto principal P corta a la semicircunferencia en el punto de vista V (en color rojo). En realidad la recta abatida LV es paralela al plano superior del prisma, como vista en un perfil, mientras que la dirección VE es paralela a la línea BF, perpendicular al plano anterior BDJG o cara superior del prisma.
Como tenemos el punto de vista V, podemos hacer centro en el punto L, intersección de la recta límite OC y la vertical LP o perpendicular a esta recta límite por el punto principal P y con el radio LV hacemos una circunferencia que corta a la línea vertical en el nuevo punto de vista abatido V1.
Haciendo centro en el punto de fuga O y con la distancia desde este punto hasta el punto de vista V1 hacemos el primer arco que corta a la recta límite en el punto métrico M2. De igual forma hacemos centro en el punto C y con la distancia desde este punto al punto de vista V1 hacemos otro arco que corta la recta límite en el punto M1.
Si consideramos el punto B como la traza de las rectas del prisma que pasan por él, alineando el punto métrico M1 con G obtenemos el punto R sobre la traza paralela por B a la recta límite. La distancia BR es en realidad la verdadera longitud de este segmento BG.
Si tomamos ahora el otro punto métrico M2, alineando el punto D con éste obtenemos en la intersección con la traza por B el punto S, la distancia SB es la longitud real del segmento DB. Hemos obtenido la verdadera dimensión de las aristas de la cara superior por el método de los puntos de medida, podríamos aplicar el mismo procedimiento para obtener las alturas de la figura, pero vamos hacerlo por dos métodos distintos, por el procedimiento directo y por el procedimiento de abatimiento.
Para construir la longitud de los segmentos verticales de la figura por el método de abatimiento, abatimos el punto de vista respecto a la recta límite EC. Para ello colocamos la longitud del punto de vista al plano del cuadro paralela a esta recta límite, entonces abatimos la semicircunferencia que pasa por los puntos O-B1 y corta a la ortogonal por el punto principal en el nuevo punto de vista abatido C1. Haciendo centro en el punto B1, que es la intersección de la ortogonal por el punto principal P a la recta límite EC, y con la distancia desde este punto hasta el punto de vista abatido C1, hacemos un arco que corta a la recta P-B1 en el punto V2, este es el nuevo punto de vista abatido respecto a la recta límite EC. Si unimos el punto de vista V2 con este punto de fuga E y por la traza de la recta B hacemos una recta paralela a esta dirección, alineando el punto F con el punto de vista V2 obtenemos en la prolongación de esta recta un punto de corte E1 con la recta anterior. La distancia B-E1 es en realidad la longitud real del segmento BF. Este segmento que hemos dibujado como un trozo más grueso y es la dimensión del segmento vertical BF, es en realidad igual al segmento azul oscuro T-A1 que vamos a determinar ahora por otro procedimiento.
Si consideramos el plano que pasa por el punto de vista perpendicular al plano del cuadro tenemos que lo corta según la recta PL. Si abatimos este plano tenemos el punto de vista de color rojo V. Si unimos este punto de vista con los puntos L E obtenemos las dos direcciones correspondientes a la cara superior del prisma y a los segmentos perpendiculares a esta cara. Por tanto habiendo considerado el punto B como punto doble, esto quiere decir el punto del prisma y al mismo tiempo su perspectiva, este punto tiene su proyección en el perfil que vamos a utilizar en T, esto es, sobre la línea perpendicular que pasa por B que corta a la recta LP. Esto quiere decir que el punto T define el perfil del punto B, por tanto por T hacemos dos rectas paralelas a las dos direcciones LV y VE. Las nuevas rectas son TW y T-A1.
Si alineamos la proyección ortogonal Z del punto F sobre el plano del perfil LP, alineando este punto Z con el punto de vista V tenemos que corta a la dirección anterior en el punto A1. Por tanto T-A1 es la longitud real del segmento BF.
Hay que decir que respecto a la imagen, fotografía o perspectiva de este prisma, como de cualquier figura, podemos obtener las dimensiones proporcionales a la figura ya que las distintas perspectivas de un objeto son homotéticas, pero como no sabemos las dimensiones del objeto no podemos obtener las medidas reales. No obstante el procedimiento nos sirve para obtener la relación entre las magnitudes de los segmentos de la figura, es como si tenemos la foto de una casa y hay que obtener sus medidas, podemos obtener todas las medidas proporcionales de la casa, pero al no tener sus dimensiones reales, desconocemos si la casa es grande, pequeña, o una maqueta. Para poder obtener las medidas reales de un objeto partiendo de una foto o un dibujo, necesitamos saber al menos una de las dimensiones de la imagen.
|
Restitución de plano inclinado
Restitución del dibujo de un automóvil.
Al lado de el dibujo del coche se ha colocado prisma para dibujar con más precisión las dos direcciones fundamentales que determinan los puntos de fuga, ya que las aristas de este prisma son paralelas a las dos direcciones del automóvil, tanto longitudinal como transversalmente. Al prolongar las aristas del prisma con las líneas fundamentales del automóvil obtenemos dos puntos de fuga F1 F2 en la intersección de cada par de aristas. Por los dos puntos de fuga pasa la línea del horizonte. Cogemos una rueda o para ser más precisos una llanta del automóvil (circunferencia cuya perspectiva es una elipse) y dibujamos dos tangentes desde el punto de fuga F2, de esta manera tenemos dos líneas horizontales que pasan por el borde inferior y superior de la llanta. De igual forma hacemos dos agentes verticales por los extremos derecho e izquierdo de la elipse, (ejercicio fácilmente resuelto considerando la polar de la elipse y el centro o polo en el infinito de esta polar).
Si construimos la diagonal del cuadrilátero que inscribe a la elipse obtenemos T en la intersección con la vertical sobre el punto de fuga F2. Haciendo centro en este punto de fuga F2 y tomando como radio la distancia desde él hasta el punto T construimos un arco hasta que corta a la semicircunferencia de diámetro F1-F2 en el punto de vista V. Uniendo el punto de vista con los puntos de fuga tenemos las dos direcciones ab en las que tenemos que colocar la planta del automóvil a partir de la traza O. Por último, alineando los puntos de la perspectiva con el punto de vista D’-V tenemos en la prolongación los puntos de la planta del automóvil, por ejemplo el punto D, de manera que todos los puntos quedan perfectamente alineados V-D-D’, conforme a la perspectiva por el método del abatimiento.
Partiendo de la planta y perfil de una figura, vamos a construir la perspectiva cónica oblicua. Colocamos en planta el plano del cuadro y la planta de la casa de forma oblicua respecto a este, prolongamos los lados de ambos cuadriláteros de la planta de la casa hasta que cortan al plano del cuadro en los puntos ABCDE. Por el punto de vista V hacemos dos rectas paralelas a estas direcciones obteniendo así en la intersección con el plano del cuadro los puntos de fuga F’1 y F’2, puntos que subimos a la línea del horizonte de la perspectiva mediante líneas perpendiculares al plano del cuadro, obteniendo así F1 F2.
De igual forma, mediante perpendiculares subimos los puntos o trazas ABCDE de las rectas a la línea de tierra hasta obtener A’ B’ C’ D’ E’. Uniendo los tres últimos puntos C’ D’ E’ con F1 tenemos ya tres rectas de la perspectiva de la planta, de igual forma uniendo los puntos A’ B’ C’ con el otro punto de fuga F2, tenemos las otras tres líneas de la planta de la casa.
Las alturas de la casa las tomamos en el perfil o en el alzado y las colocamos a partir de las trazas de las rectas sobre la línea de tierra, por ejemplo, sobre la recta s’, perspectiva de la recta s, tomamos la distancia d1 y el vértice superior de este segmento lo unimos con el punto de fuga F2 de esta recta, donde corta a la vertical de la arista de la casa, obtenemos la altura en la dimensión correspondiente de la perspectiva. De igual forma obramos con las demás alturas, por ejemplo la dimensión d2 la colocamos a partir de la traza de la recta t’ y el extremo superior lo unimos con el punto de fuga F2, donde corta a las verticales de la planta en perspectiva obtenemos la altura de la casa correspondiente a esta dimensión.
El punto de fuga de las líneas oblicuas del tejado se cortan en F3, siempre sobre la vertical que pasa por el punto de fuga F1, ello es debido a que está en el mismo plano vertical que la recta C’-F1 y por tanto su recta límite o de horizonte es la misma, esto es, la línea vertical que pasa por el punto de fuga F1.
Restitución de la pendiente del tejado.
Si tenemos la fotografía de la casa o dibujo de la misma y está en perspectiva, para obtener el ángulo g que forma el plano del tejado con el plano horizontal, dibujamos una semicircunferencia cuyo diámetro serán los puntos F1 F2, por el punto principal P hacemos una ortogonal a la línea del horizonte hasta que corta a esta semicircunferencia en el punto de vista abatido (V). Haciendo centro en F1 y con la distancia del radio del nuevo arco F1-(V) hacemos un arco hasta que corta a la línea del horizonte en el punto (V’). Si unimos este punto con el punto de fuga F3 de las líneas del tejado, tenemos que esta recta y la del horizonte forman un ángulo g, que es realmente el ángulo del tejado con un plano horizontal. |